, где 
- число фаз обмотки статора. Из Электромагнитный момент и угловые характеристики
При рассмотрении принципа работы синхронных машин было установлено, что
вращающий момент является синусной функцией угла нагрузки q . Этот же результат можно получить из баланса мощностей машины.Активная мощность, потребляемая машиной из сети равна , где - число фаз обмотки статора. Из
. Кроме того, из прямоугольных треугольников abc и adc получим 
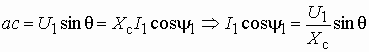. Отсюда активная мощность 
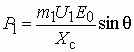. Если пренебречь относительно небольшими тепловыми потерями в статоре, то активная мощность будет равна электромагнитной мощности, т.е. мощности передаваемой магнитным полем из статора в ротор 
, где 
- синхронная угловая частота вращения ротора, 
- угловая частота питающей сети, а p - число пар полюсов машины. Отсюда вращающий момент синхронной машины равен
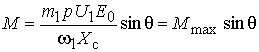. При постоянном напряжении сети максимальный момент машины зависит только от ЭДС потока ротора, т.е. от величины тока возбуждения.
В случае явнополюсной машины индуктивное сопротивление реакции якоря по продольной 
и поперечной оси 
будут разными 
. Соответственно разными будут и синхронные сопротивления по этим осям – 
и 
. Подставляя эти выражения в уравнение момента, получим
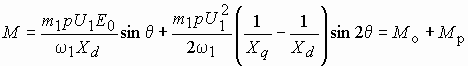
Это выражение справедливо для любого типа ротора как явнополюсного, таки неявнополюсного. У неявнополюсного ротора 
. Тогда второе слагаемое обращается в нуль, и мы придем к полученному ранее выражению. Таким образом, в случае магнитной асимметрии ротора электромагнитный момент складывается из двух составляющих: основного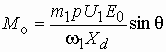 
и реактивного 
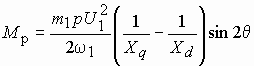моментов.
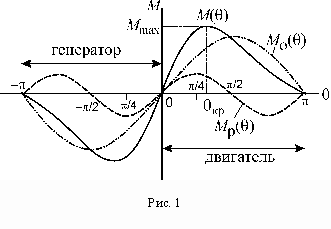
Зависимость электромагнитного момента машины от угла нагрузки называется угловой характеристикой. В общем случае она представляет собой сумму двух синусоид основного и реактивного моментов показанных на рисунке 1. Максимум основного момента приходится на угол
, а реактивного – 
Участки характеристики с положительной производной 
соответствуют устойчивым режимам работы машины, т.е. углам нагрузки 
. На этих участках увеличение момента нагрузки вызывает увеличение угла нагрузки и соответственно электромагнитного момента вплоть до статического состояния, когда момент нагрузки будет уравновешен моментом машины. На участках с 
увеличение угла нагрузки будет приводить к снижению электромагнитного момента и увеличению рассогласования с моментом на валу. Если при этом момент нагрузки не превышает максимального момента машины, то ротор повернувшись чуть более чем на пол-оборота придет в точку статического равновесия на устойчивом участке угловой характеристики.
Очевидно, что синхронная работа машины возможна только если нагрузочный момент не превышает максимальный 
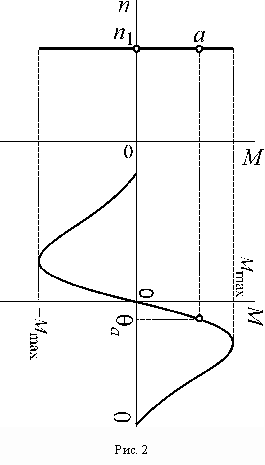
Механическая характеристика синхронной машины показана на рис. 2. Она представляет собой отрезок прямой линии, проходящий через точку синхронной скорости 
параллельно оси момента и ограниченный значениями угловой характеристики. Для каждой точки механической характеристик можно определить угол нагрузки, спроектировав эту точку на участок устойчивой работы обращенной угловой характеристики.