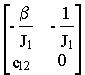
Лекция 9
АНАЛИЗ ДЕМПФИРУЮЩЕГО ДЕЙСТВИЯ ЭМП НА КОЛЕБАТЕЛЬНОСТЬ ЭМС С ДВУХМАССОВОЙ МОДЕЛЬЮ МЕХАНИЗМА
При решении любых задач нужно уметь оценить влияние упругих связей на динамику ЭМС. Здесь мы проведем анализ особенностей вза-имодействия ЭМП с линейной механической характеристикой с меха-низмом, представленным двухмассовой моделью в единой ЭМС.
Возьмем за основу систему “ЭМП- механизм”, описываемую уравнениями
dM/dt = (
b / Tэ) w 0- (b / Tэ)w 1 -(1/ Tэ)M,d
w 1/dt= - (1/ J1) M12 +(1/ J1) M -(1/ J1) Mc1 ,dM12 /dt =C12
w 1 - C12 w 2,d
w 2/dt= (1/ J2) M12 - (1/ J2) Mc2.Если пренебречь электромагнитной инерцией ЭМП, т.е. предположить, что Tэ =0 и рассматривать только свободное движение в системе (
w 0=0) , то первое уравнение системы превращается в алгебраическое и из него следует, чтоM=-
b w 1 .Следовательно, при отсутствии электромагнитной инерции ЭМП создает воздействующий на первую массу механизма момент, аналогичный моменту вязкого трения ( момент, пропорциональный скорости). Значит, благодаря наличию электромеханической связи ЭМП должен оказывать на колебания в механической подсистеме демпфирующее воздействие, аналогичное действию сил вязкого трения.
Оценим такое воздействие в системе с J
2 >> J1 при w2 @ 0 , что равносильно жесткой заделке второй массы. Такая система может быть описана парой уравненийd
w 1/dt= - (1/ J1) M12 +(1/ J1) M -(1/ J1) Mc1 ,dM12 /dt =C12
w 1 - C12 w 2 ,с учетом принятых допущений принимающих вид
d
w 1/dt= -(b / J1) w 1 - (1/ J1) M12 -(1/ J1) Mc1,dM12 /dt =C12
w 1 - 0 w 2.Матрица
A, характеризующая свободное движение системы и характеристическое уравнение det ( l1 - A)=0 имеют вид соответственноA= 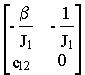
и
![]() .
.
Вводя понятие собственной резонансной частоты первой массы при жесткой заделке второй
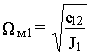 ,
,
перепишем характеристическое уравнение так
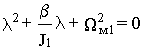 .
.
Следовательно, собственные числа системы определяются выражением
 .
.
Анализируя последнее выражение, легко установить, что при жесткости
b электромеханического преобразователя, отличной от нуля, свободное движение системы является принципиально затухающим. При условии![]() или b і 2 c12
или b і 2 c12
свободное движение в системе носит апериодический характер, поскольку собственные числа являются вещественными. При условии
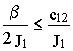 или b Ј 2 c12
или b Ј 2 c12
собственные числа становятся комплексно-сопряженными и определяются выражением
l
1,2=-d ± jW св,где
W св=Ц Wм12- d 2, d = b /2 J1 и Wм1=Ц c12/J1.Следовательно, свободная составляющая процесса носит колебательный затухающий характер с частотой свободных колебаний
Wсв и экспоненциальной огибающей, обладающей постоянной времени 1/d = b /2J1 . Логарифмический декремент затухания определяется выражениемn
= d Tсв= 2p d / Ц W м12- d 2С ростом жесткости механической характеристики
b ЭМП уменьшается время затухания, падает частота свободных колебаний. и возрастает логарифмический декремент затухания.Зависимость
n (b ) для рассматриваемого случая представлена кривой 1 на рис. 9.1. При увеличении b от 0 до некоторого значения bкр затухание колебаний постепенно увеличивается и при b=bкр переходный процесс в системе приобретает апериодический характер (n =Ґ ) . Это значение равно bкр = 2 c12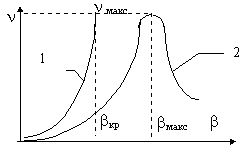
Рис.
9.1.Таким образом, изменение жесткости механической характеристики ЭМП является эффективным средством изменения колебательности системы.
При конечных значениях J
2 и g =(J1+J2)/J1 c ростом b в процесс колебаний вовлекается вторая масса, причем при b =Ґ (что соответствует жесткой заделке первой массы) колебания становятся незатухающими. Следовательно, если принять, что b ® Ґ , то в двухмассовой системе демпфирование должно уменьшаться и n ® 0 . Несомненно , что существует такое значение b = bмакс, при котором декремент затухания достигает максимума n (bмакс) = nмакс (см. кривую 2 на рис.9.1.) Величина последнего зависит от конкретного сочетания параметров электромеханической системы. При предельно слабой электромеханической связи (b = 0) и при предельно сильной связи (b = Ґ) демпфирование отсутствует (n = 0).Электромагнитная инерция ЭМП, характеризуемая постоянной времени Tэ, также влияет на величину демпфирования, при этом и зависимость
n ( Tэ ) не является однозначной. Изменение Tэ в определенных пределах позволяет увеличить n по сравнению с ранее рассмотренным случаем Tэ=0.