Лекция 6
ДИНАМИЧЕСКИЕ СВОЙСТВА МЕХАНИЧЕСКОЙ
ПОДСИСТЕМЫ ЭМС
В этом разделе мы рассмотрим механическую часть обособленно от электрической части с целью изучения ее динамических свойств. Входным воздействием этой подсистемы будем считать электромагнитный момент M и задавать его независимой функцией времени. Переходные процессы в подсистеме, обусловленные изменением этого момента, называются механическими
переходными процессами.Уравнения состояния и собственные числа подсистемы
Процессы в указанной подсистеме описываются уравнениями 5.2 а,б,в.
d
w 1/dt= - (1/ J1) M12 +(1/ J1) M -(1/ J1) Mc1dM12 /dt =C12
w 1 - C12 w 2d
w 2/dt= (1/ J2) M12 - (1/ J2) Mc2Принимая в качестве вектора состояния вектор
Yт =[ w 1 M12 w 2 ] , в качестве вектора управления - трехмерный вектор Uт = [ M Mc1 Mc2 ] и качестве выходных переменных сами переменные состояния , получим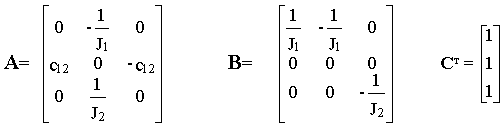
Этой системе уравнений соответствует приведенная на рис.6.1 ДСС.
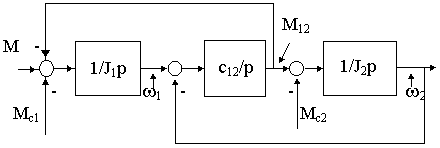
Рис. 6.1.
Определим собственные числа матрицы
A из характеристического уравнения подсистемыdet(p1 - A)=0
или для данного случая
det (p1-
A)= det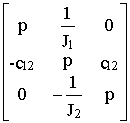 =0
=0
Раскрывая определитель, получим
![]()
или
![]()
Как видно, среди собственных чисел или корней характерис-тического уравнения подсистемы имеется один нулевой (p
1=0) и пара чисто мнимых корней видаp23=
± j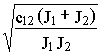
Вводя понятие резонансной частоты двухмассовой упругой механической системы
W
0=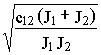 ,
, получим p
23=± jW 0 и следовательно,det(p1 - A)= ![]()
Корни характеристического уравнения свидетельствуют о том, что:
Передаточные функции и частотные характеристики механической подсистемы
Найдем передаточную матрицу подсистемы по известному правилу.
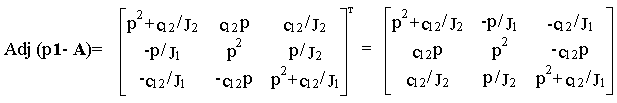
Поскольку
Cт=[ 1 1 1] , тоH
(p)= G(p) = (p1-A)-1 B=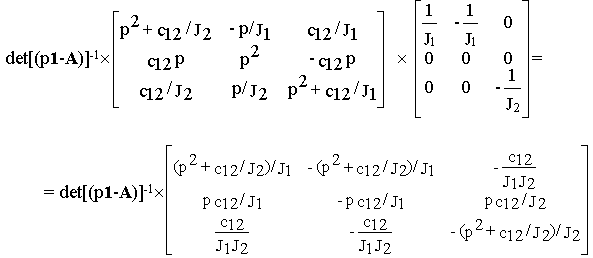
Нас будут интересовать передаточные функции каналов M
® w 1 и M® w 2. Из полученной передаточной матрицы находимW
w 1M(p)= w 1(p)/M(p)=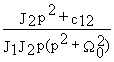
и
W
w 2M(p)= w 2(p)/M(p)=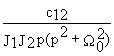
С учетом выражения (6.1) искомые передаточные функции приведем к виду
W
w 1M(p)=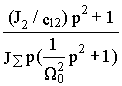
и
W
w 2M(p)=
Введем понятие соотношения масс
g = (J1+J2)/J1. Тогда выражение для передаточной функции Ww 1M(p) принимает видW
w 1M(p)=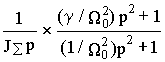
Последняя в соответствии с полученной передаточной функцией может быть представлена последовательным соединением интегрирующего звена, форсирующего звена второго порядка с сопрягающей частотой ![]() и консервативного колебательного звена с сопрягающей частотой
и консервативного колебательного звена с сопрягающей частотой
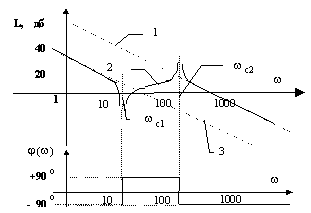
Рис. 6.2.
Амплитудно -частотная характеристика претерпевает разрыв на двух частотах ![]() и
и
В низкочастотной области сдвиг по фазе между колебаниями определяется интегрирующим звеном и составляет 90 град. При![]() фазовый сдвиг уменьшается скачком на 180 град, т.е. достигает значения +90 град и на частоте
фазовый сдвиг уменьшается скачком на 180 град, т.е. достигает значения +90 град и на частоте
Как видно, движение первой массы при небольших частотах колебаний управляющего воздействия M определяется суммарным моментом инерции J
S , причем механическая часть ведет себя как интегрирующее звено. Иными словами, интегрирующее звено характеризует условия движения механической части в среднем.При приближении частоты колебаний момента к резонансной амплитуда колебаний скорости
w 1 возрастает и при w =W 0 стремится к бесконечности. Однако проявления резонанса существенно зависят от параметров механической в связи с наличием в числителе передаточной функции Ww 1M(p) форсирующего звена второго порядка. Можно выявить условия, при выполнении которых влияние упругости на движение первой массы будет незначительным. К их числу относятся:1.
J2< < J1. При этом g ® 1 , полиномы в числителе и знаменателе передаточной функции сокращаются и передаточная функция системы определяется передаточной функцией интегрирующего звена, т.е.W
w 1M(p)=1/ JS p2. .
W0 >> wср , где wср - частота среза желаемой ЛАХ разомкнутого контура регулирования, При этом условии в области малых и средних частот движение первой и второй массы определяется тем же интегрирующим звеном. Отсюда вытекает важный практический вывод:Если при синтезе ЭМС используются обратные связи только по переменным двигателя, то при
J2< < J1 или W 0> > w ср , механическую часть ЭПС можно представлять жестким механическим звеном, не учитывая влияния упругости.На рис. 6.3 представлены ЛФЧХ подсистемы с выходной переменной w 2 и полученной выше передаточной функцией (6.5)
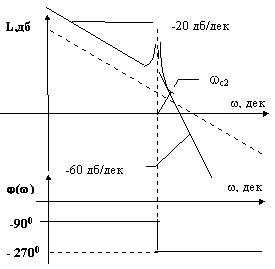
Рис. 6.3.
Эта передаточная функция отличается от рассмотренной выше лишь числителем, который равен единице на всех частотах. Амплитудная характеристика имеет разрыв только на частоте
W 0 и в высокочастотной области стремится к ассимптоте с наклоном -60 дб/дек. Соответственно фазовый сдвиг между колебаниями стремится к величине -270 град.В соответствии с выражением для W
w 2M(p) колебательность второй массы выше, чем первой. В низкочастотной области ЛАХ обоих систем совпадают, так как в среднем движение второй массы определяется тем же интегрирующим звеном. Однако при w > W 0 наклон высокочастотной ассимптоты составляет -60 дб/дек и нет факторов, которые ослабляли бы развитие резонансных колебаний при любых g . Следовательно :Во всех случаях, когда важно получить требуемое качество движения второй массы, а также при регулировании ее координат, пренебрегать влиянием упругостей механических связей нельзя.
В реальных системах присутствуют диссипативные силы, которые оказывают демпфирующее воздействие на колебательную систему ( например, внутренние силы вязкого трения) Но это демпфирование в большинстве случаев невелико. Оно существенно не сказывается на частотных характеристиках, однако ограничивает резонансные пики конечными значениями и несколько сглаживают фазочастотные характеристики.
Нетрудно установить, что частотные характеристики абсолютно упругой системы, приводимой к одномассовой , совпадают во всем диапазоне с частотными характеристиками идеального интегрирующего звена, а структурная схема принимает вид
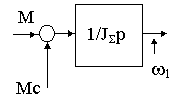
Механические переходные процессы
Изменение управляющего или возмущающих воздействий вызывают в механической подсистеме переходные процессы, называемые механическими переходными процессами.
Рассматривая одномассовую систему, движение которой описывается дифференциальным уравнением первого порядка
J
S dw /dt= M- Mc,где J
S = J1+J2 и Mc= Mc1 + Mc2,легко установить, что при постоянстве статического момента сопро-тивления закон изменения скорости в переходном процессе определяется характером изменения во времени управляющего момента. Так для получения экспоненциальной кривой скорости при пуске необходимо обеспечить экспоненциальную зависимость момента от времени. Для получения равномерно ускоренного изменения скорости необходимо формировать прямоугольный закон изменения момента двигателя во времени (см. рис. 6.4,а,б ).
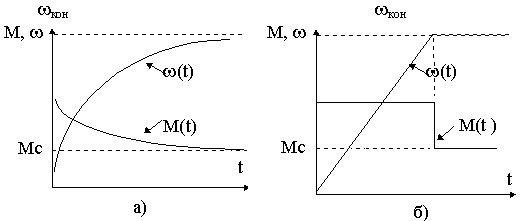
Рис.6.4
Если известен характер изменения момента двигателя и приведенного момента нагрузки с помощью указанного уравнения можно установить характер изменения скорости не прибегая к его решению. Механическая часть, представленная в виде жесткого звена, как отмечалось, отражает движение системы в среднем и не дает точного представления о характере движения упруго связанных масс. С целью выяснения этого влияния рассмотрим реакцию на скачок момента от 0 до M в двухмассовой системе при нулевых нагрузках M
c1 и Mc2 и нулевых начальных условиях.Найдем вначале реакцию координаты
w 2 , используя ранее полученную передаточную функцию (6.5). Операторное изображение интересующей нас величины при M(p)= M/p равноw
2(p)=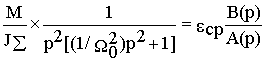 ,
,
где
e ср - среднее значения ускорения второй массы, B(p)=1 иA(p)= p2[(1/
W 02)p2+1] - полином с корнями p1,2 =0 и p3,4=± jW 0Решение найдем по формуле разложения в виде суммы двух составляющих
w
2(t) = w ‘(t) +w “(t),первая из которых обусловлена парой нулевых корней, а вторая- парой комплексно-сопряженных корней.
Пользуясь модификацией формулы разложения для случая
n кратных корней полинома знаменателяx(t)= 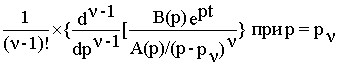
получим
w
‘(t) =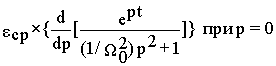
или
w
‘(t) =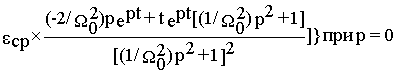
После подстановки p=0, получим
w
‘(t)= e ср t.Из курса математики известно, что пара комплексно сопряженных корней p
i,i+1 определяет во временной области составляющую решения видаx(t)= 2Re 
В нашем случае
A’(p)=dA(p)/dp= -2j
W 02и потому
w
“(t)= e ср ґ 2Re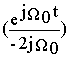 = -(e ср/W 0) Sin W 0t
= -(e ср/W 0) Sin W 0t
Таким образом получили окончательное решение
w
2(t) = w ‘(t) +w “(t) = e ср t -(e ср/W 0) Sin W 0tГрафик зависимости
w 2(t) представлен на рис.6.5.. Видно, что скорость w 2 (t) в среднем меняется по линейному закону с ускорением e ср=M/JS и содержит незатухающую гармоническую составляющую с амплитудой e ср/W 0 и частотой W 0 .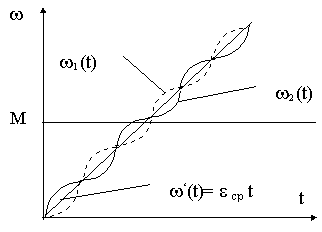
Рис.6.5
Определим теперь скорость первой массы, используя выражение для передаточной функции (6.4), которое можно представить в виде суммы
W
w 1M(p)= Ww 2M(p)+ ,
,
первое слагаемое которой является передаточной функцией W
w 2M(p).Следовательно, решение
w 1(t) будет содержать три составляющие , две из которых w ‘(t) и w"(t) нами уже найдены, а третье можно определить из выраженияw
‘’’(t) =L-1 {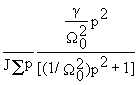 ґ M/p }
ґ M/p }
или
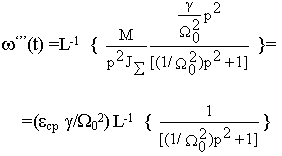
Принимая В(P)=1 и A’(p)= p(2/
W 012) и при p=j/W 0 A’(jW 0)= 2j/W 0, получим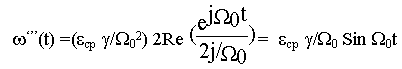
Эта составляющая отмечена штриховой линией на уже рассмот-ренном рисунке. Она находится в противофазе с колебаниями
w ’’(t) и потому колебания скорости w 1(t) меньше, чем w 2(t). При прочих равных условиях колебания скорости w 1(t) тем меньше, чем меньше J2, а увеличение W 0 при тех же ускорениях снижает амплитуды колебаний как первой, так и второй массы. Эти выводы полностью согласуются с результатами частотного анализа. Под действием сил внутреннего вязкого трения эти колебания в действительности являются затухающими во времени, однако время затухания достаточно велико.