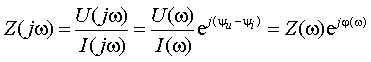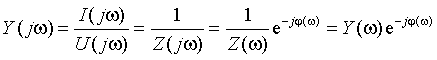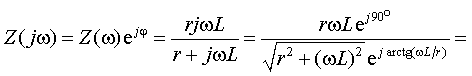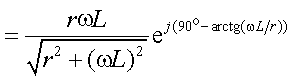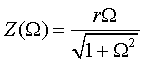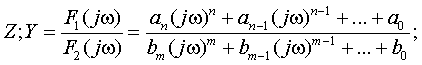1.1
Частотные характеристики двухполюсников
Пассивные
двухполюсники и четырехполюсники включают набор резистивных и реактивных
(индуктивных и емкостных) элементов, в которых протекают электрические токи под
действием какого-либо одного внешнего источника энергии. Для описания
физических явлений в таких цепях при воздействии на входных зажимах источника
гармонических колебаний с фиксированной частотой 
=const используют метод комплексных амплитуд, который в свою
очередь основывается на введении понятий комплексных сопротивлений или
проводимостей отдельных элементов цепи -r,
,
, а также комплексных амплитуд токов и
напряжений – 
, 
[1].
В общем случае у источника гармонических
колебаний может изменяться не только амплитуда и начальная фаза, но и угловая
частота - 
. Тогда комплексная характеристика источника (входного
воздействия) записывается в виде функции мнимой комплексной переменной - 
(
). Эту характеристику обычно записывают в показательной
(полярной) форме и называют комплексной спектральной плотностью. Модуль этой
характеристики называют спектральной плотностью, а аргумент - фазовой
плотностью или фазочастотной характеристикой. Так для напряжения 
имеем:
|
|
где 
- спектральная
плотность напряжения, 
- фазовая плотность
напряжения.
Аналогично гармонический ток с переменной
угловой частотой ω
характеризуется своей комплексной спектральной плотностью:
|
|
В
зависимости от вида входного воздействия (электрического сигнала) спектральные
плотности могут иметь непрерывный или дискретный характер. В дальнейшем для
краткости будем опускать написание зависимости от угловой частоты, полагая 
, 
, 
, 
.
В реальном двухполюснике или
четырехполюснике комплексные плотности токов и напряжений связаны между собой
соотношениями, зависящими как от внутренних свойств элементов цепи, так и от
способа соединения ветвей. Подобного рода соотношения называются частотными
характеристиками.
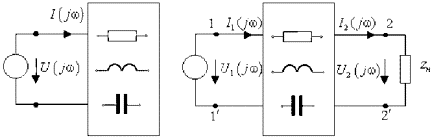
На рис.1.1а изображен двухполюсник, имеющий два входных
зажима, к которым подсоединяется источник входного сигнала. Если к цепи присоединяется
источник тока J(t), то входной ток i(t) = J(t), т.е. будет независимой функцией
времени, а напряжение u(t) на входе определится через свойства
цепи как зависимая функция. При гармоническом характере входного сигнала
определяют отношение комплексов напряжения и тока.
|
|
(1.1) |
Такое отношение называют
комплексным входным сопротивлением
двухполюсника:
Из определения (1.1) следует, что Z(jω)
в свою очередь включает две характеристики: 
-
амплитудно-частотную характеристику (АЧХ) и 
- фазочастотную характеристику (ФЧХ) функции входного
сопротивления.
а) б)
Рис.
1.1. Обобщенная комплексная схема замещения цепи:
а)
двухполюсника; б) четырехполюсника
Если к цепи присоединяется источник
напряжения e(t), то напряжение на двухполюснике u(t) = e(t),
т.е. будет независимой функцией времени, a ток i(t) определится через свойства
цепи как зависимая функция. При гармоническом характере входного сигнала
определяют отношение тока к напряжению, которое называют комплексной входной
проводимостью двухполюсника:
|
|
где Y(ω) и φ(ω) называют
соответственно АЧХ и ФЧХ функции входной проводимости.
Функции Z(jω)
и Y(jω) являются взаимно обратными функциями. В определении этих
функций входят токи и напряжения, что дает возможность находить эти
характеристики опытным путем, используя вольтметр, амперметр и прибор,
измеряющий фазу гармонического колебания. Однако сами функции в силу линейности
рассматриваемых цепей не зависят от величин токов и напряжений и могут быть
определены непосредственно по структуре (топологии) цепи с учетом характера
элементной базы ветвей. Для нахождения этих характеристик могут быть
использованы все известные методы расчета цепей постоянного тока: законы
Кирхгофа, простейшие преобразования, упрощающие схему и т.п. [1]. Исследование
этих характеристик позволяет предсказать поведение цепи при различного рода
воздействиях, о чем будет сказано далее.
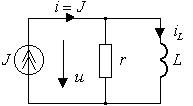
Пример 1.1.
Найти АЧХ и ФЧХ для функции входного сопротивления двухполюсника, образованного
параллельным соединением резистивного и индуктивного элемента (рис.1.2а).
Питание цепи осуществляется от источника синусоидального тока 
с любой частотой.
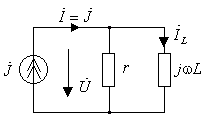
а) б)
Рис.
1.2. Схема для исследования входного сопротивления двухполюсника:
а)
исходная схема; б) комплексная схема замещения
Решение задачи начинаем с построения
комплексной схемы замещения исходной цепи (рис. 1.2б), на входе которой
действует комплексный спектр источника тока I(jω) = J(jω), в результате чего
на двухполюснике будет иметь место комплексный спектр напряжения U(jω).
Отношение их, определяемое выражением (1.1), может быть найдено непосредственно
по структуре цепи путем объединения комплексных сопротивлений параллельно
соединенных ветвей:
|
|
|
|
Сравнивая модули и аргументы, запишем АЧХ
и ФЧХ
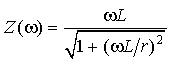- АЧХ функции входного
сопротивленияисследуемого выражения
φ(ω) = 
- ФЧХ функции входного сопротивления.
При построении графиков целесообразно перейти к относительной
переменной Ω = ωL/r, которая указывает во сколько раз
сопротивление индуктивности на данной частоте больше резистивного
сопротивления. Для
этой переменной полученные выше выражения
перепишутся в виде
|
|
|
Графики найденных функций представлены на
рис.1.3а и рис.1.3б в относительных масштабных единицах.
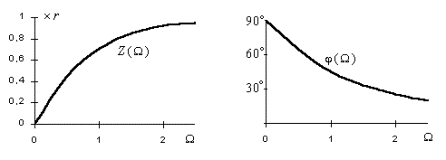
а) б)
Рис.
1.3. Частотные характеристики функции входного сопротивления: а)АЧХ; б)ФЧХ
Расчетные значения сведены в таблице 1.
Таблица
1
|
|
|
|
градусы |
|
|
0 |
1.0 |
0 |
0 |
90 |
|
0.5 |
1.12 |
0.447r |
26.5 |
63.5 |
|
1.0 |
1.41 |
0.707r |
45.0 |
45.0 |
|
1.5 |
1.80 |
0.832r |
56.3 |
33.7 |
|
2.0 |
2.23 |
0.894r |
63.4 |
26.6 |
|
2.5 |
2.69 |
0.928r |
68.2 |
21.8 |
|
|
|
r |
90 |
0 |
Для перехода к реальной частоте
необходимо знать численные значения параметров цепи r и L .Тогда переход
осуществляется по формуле ω = r/LΩ (рад/с), если L измеряется в генри, а r в омах.
Из
рассмотренного примера следует, что для нахождения аналитического выражения Z(jω)
или Y(jω) как функции частоты следует задать входное напряжение U (или входной ток I) и найти входной ток I
(или входное напряжение U), затем
воспользоваться одним из выражений Z = U/I или Y = I/U.
Если известна структура и характер
элементов цепи, то искомое выражение можно найти непосредственно, как это было
сделано в примере 1.1. Полученное выражение обычно приводят к виду
|
|
где 
и 
полиномы, зависящие
от переменной w.
После преобразований с комплексными слагаемыми всегда есть возможность записать
исследуемую функцию в полярной (показательной) форме, выделяя зависимости АЧХ и
ФЧХ.
В простейших неразветвленных rL и rС
цепях иногда используют понятие граничной частоты 
. Граничной называется частота, при которой r = X, т.е. 
= r/L, или 
= 1/rС. Как следует
из приведенного выше примера 1.1, на граничной частоте Z(ω) = 0.707r, а φ(ω) = 45˚.
Задача решена.