Введение

Предмет макроскопической электродинамики составляет изучение электромагнитных полей в пространстве, заполненном веществом. Вид уравнений макроскопической электродинамики и смысл входящих в них величин существенно зависят от физической природы материальной среды, а также от характера изменения поля со временем. В общем случае все электромагнитные поля описываются полной системой уравнений Максвелла, которую записывают в дифференциальной и интегральной форме:

Дифференциальная форма Интегральная форма

; ; .

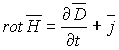
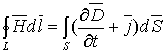
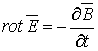
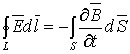
Эти уравнения являются исходными при изучении теории электромагнитного поля. Если свойства среды, определяемые коэффициентами , , g, неизменны, то все записанные уравнения будут линейными. Как известно, сумма частных решений системы линейных дифференциальных уравнений также является его решением. Иными словами, если известен ряд полей , ; , ; , и так далее до , , которые определяют поля от отдельных источников поля, то может существовать результирующее суммарное поле и . Этому положению соответствует принцип суперпозиции, согласно которому поле, образованное несколькими источниками, представляет собой сумму полей каждого из источников, существующего в тех же условиях отдельно.

При изучении электромагнитных полей различных типов стараются ввести понятие потенциальной функции (потенциала) поля - j (или U), которая является скалярной характеристикой векторного поля. Для этой функции также выполняется принцип суперпозиции (наложения): результирующий потенциал системы источников поля складывается из потенциалов отдельных источников.

Все электромагнитные поля разбиваются на классы. Простейшими являются неизменные во времени поля – статические (электростатические и магнитостатические), а также стационарные и квазистационарные поля. К ним следует отнести электрическое поле постоянных токов. Эти классы полей рассматриваются в пособии.

В добавление к тому, что известно в учебной литературе, настоящее пособие ориентирует читателя на использование возможностей персональной вычислительной техники - пакета программ MathCAD и программного комплекса ELCUT, представляющего собой интегрированную диалоговую систему программ, позволяющую решать плоские и осесимметричные задачи любых потенциальных полей. Использование этих пакетных программ даёт возможность говорить о законченной форме изучения такого сложного курса как Теория электромагнитного поля, исследовать дифференциальные и интегральные инженерные характеристики решенной задачи.