4.
Использование пакета ELCUT для решения задач
электростатики
4.1.
Постановка задачи электростатики в ELCUT
Анализ электрического и магнитного поля необходим как в специальном приборостроении, так и при проектировании сильноточного высоковольтного оборудования (разрядников, выключателей, элементов линий электропередачи), изоляционных конструкций, кабелей, конденсаторов, а также при исследовании структуры TEM-волн в волноводах. Обычно представляют интерес следующие физические величины: электрический потенциал, напряженность поля, электрическое смещение (индукция), заряд, емкость и сила взаимодействия заряженных объектов.
Постановка задачи электростатики: ELCUT может применяться для анализа линейных
электростатических полей в плоской и осесимметричной постановках. Задача
формулируется в виде уравнения Пуассона относительно скалярного электрического
потенциала 
. Для плоскопараллельных задач уравнение имеет вид:
,
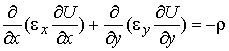а для осесимметричных задач:
,
где компоненты тензора электрической проницаемости 
, 
или 
, 
, а также плотность распределенного заряда 
- постоянные величины
в пределах блоков модели. Для большинства задач свойства среды считаются
одинаковыми во всех направлениях.
Свойства сред: изотропные и ортотропные материалы с постоянной диэлектрической
проницаемостью.
Источники поля в электростатике: распределенные и точечные заряды, электроды с
заданным потенциалом. ELCUT обеспечивает возможность задать электрический заряд
в блоках, на рёбрах и в отдельных вершинах модели. Заряд, заданный в конкретной
точке плоскости xy, описывает
заряженную струну (линейный провод), проходящую через эту точку перпендикулярно
к плоскости модели, и задается своей линейной плотностью. В осесимметричном
случае заряд вершины описывает заряженный линейный провод в форме кольца, ось
которого совмещена с осью z,
или точку (точечный заряд) на оси
симметрии. Чтобы охватить оба этих случая, точечный источник поля, заданный в
вершине, всегда характеризуется полным зарядом. Для заряженного кольца радиуса r полный заряд связан с
линейной плотностью соотношением 
. Линейная плотность заряда на ребре модели соответствует
заряженной поверхности в трехмерном пространстве. Такое ребро описывается
поверхностной плотностью заряда и задается при помощи граничного условия
Неймана для ребра. Плотность заряда, ассоциированного с блоком, соответствует объемному
заряду.
Граничные условия в электростатике: На внутренних и внешних границах области
допустимы следующие виды граничных условий.
Условие Дирихле задает известное значение электрического потенциала 
в вершине или на
ребре модели (например, на обкладках конденсатора). Этот вид граничного условия
также может применяться на внешней границе области, совпадающей с плоскостью
электрической антисимметрии задачи (противоположные по знаку источники в
симметричной геометрии). Величина 
на ребре модели может
быть задана в виде линейной функции координат. Параметры задающей линейной
функции могут меняться от ребра к ребру, но должны быть согласованы так, чтобы
функция 
была непрерывна в
точках соприкосновения границ.
Замечание. Для того чтобы задача была сформулирована корректно, необходимо
задание условия Дирихле хотя бы в одной точке расчетной области, а если область
представляет собой набор физически не связанных подобластей - хотя бы в одной точке
каждой такой подобласти. Это условие позволяет однозначно определить начальную точку отсчета потенциальной функции.
Условие Неймана – заданные значения нормальной составляющей поля, определяются
следующими соотношениями:
- на внешней границе,
- на
внутренней границе,
где 
нормальная компонента
электрического смещения, индексы "+" и "-" означают "слева от границы"
и "справа от границы" соответственно, 
- поверхностная
плотность заряда (см. также раздел 1.1 формулы 1.6 – 1.8).
Если 
принимает нулевое
значение, граничное условие называется однородным,
что означает отсутствие нормальной компоненты напряженности электрического
поля. Этот вид граничного условия часто используется на внешней границе
области, являющейся следом плоскости симметрии задачи. Однородное условие
Неймана является естественным, оно
устанавливается по умолчанию на всех рёбрах внешней границы, где явно не
указано иное граничное условие.
При задании неоднородного условия Неймана на внешней границе, являющейся следом плоскости
симметрии, истинную величину плотности заряда следует разделить пополам.
Граничное условие равного потенциала используется для описания изолированных проводников,
помещенных в электрическое поле, которые имеют постоянный, но заранее
неизвестный потенциал.
Замечание. Ребро, на котором задано условие равного потенциала, не должно
соприкасаться с рёбрами или вершинами, на которых задано условие Дирихле. В
этом случае ребро с постоянным потенциалом следует описать при помощи условия
Дирихле с подходящим значением потенциала.
Вычисляемые физические величины в электростатике: При анализе результатов
расчета электрического поля ELCUT позволяет оперировать со следующими
локальными и интегральными физическими величинами.
Локальные величины:
· Скалярный электрический потенциал 
;
· Вектор напряженности электрического поля 
,
, 
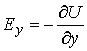- в
плоском случае,
, 
- в осесимметричном случае.
· Тензор градиента напряженности электрического поля
,
, 
, 
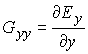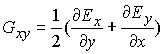- в
плоском случае,
, 
, 
- в осесимметричном случае,
а также его главные компоненты.
· Вектор электрического смещения 
.
Интегральные величины:
· Суммарный электрический заряд, заключенный в
заданном объеме:
,
где интегрирование ведется по поверхности окружающей
заданный объем, а n - единичный вектор нормали к поверхности;
· Суммарная электростатическая сила, действующая на
тела, заключенные в заданном объеме:
,
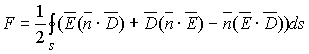· Суммарный момент электростатических сил,
действующих на тела, заключенные в заданном объеме:
,
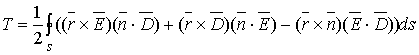где 
- радиус-вектор точки интегрирования. Вектор
момента направлен параллельно оси z в
плоско-параллельном случае, а в осесимметричном случае момент тождественно
равен нулю. Момент рассматривается относительно начала координат. Момент
относительно произвольной точки может быть получен прибавлением слагаемого 
, где 
- это полная сила, а 
- радиус-вектор точки.
· Энергия электрического поля:
.
В плоскопараллельной
постановке интегральные характеристики вычисляются на единицу длины расчетной
области в направлении оси z. Область
интегрирования задается в плоскости модели замкнутым
или разомкнутым контуром, состоящим
из отрезков и дуг окружностей.
Специальные возможности: Интегральный калькулятор может вычислять различные
интегральные значения на определенных пользователем линиях и поверхностях. В
задачу могут быть включены изолированные проводники с заранее неизвестным
потенциалом (электростатические экраны). Электростатические силы могут быть переданы
в задачу расчета механических напряжений в элементах конструкции (совмещенная
электро-упругая задача).
4.2. Пример
решения задачи электростатики в ELCUT
В качестве примера
рассмотрим задачу из раздела 1.6. Приведем подробные пошаговые инструкции с описанием
того, как можно создать и решить эту задачу.
Запустим файл ElcutStudent.exe из Проводника Windows или любой другой оболочки.
Откроется главное окно ELCUT.
1. Создание
новой задачи
1.1. Нажимаем одновременно
комбинацию клавиш Ctrl+N или левой кнопкой мыши
вызываем меню Файл, из развернувшегося списка меню Файл выбираем команду
“Создать”. Появляется окно “Новый документ” (рис. 4.1). По умолчанию выделено
“Задача ELCUT” (для выбора другого типа документа ELCUT следует
щелкнуть на нем левой кнопкой мыши). Выбираем левой кнопкой мыши пункт “Готово”.
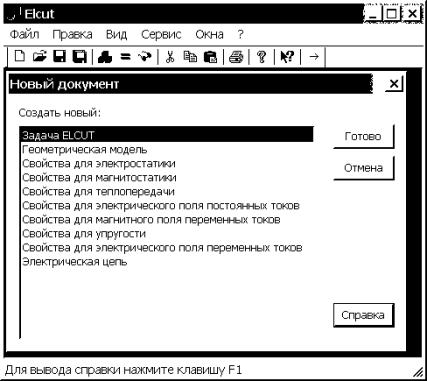
Рис. 4.1. Окно создания нового документа ELCUT
1.2. Появляется новое окно
“Создание задачи”, приглашающее ввести имя и расположение новой задачи. Вводим c
клавиатуры в графе “Имя файла задачи” имя новой задачи (например: electro_01).
Выбираем левой кнопкой мыши пункт “Обзор” и определяем месторасположение новой
задачи, где ELCUT будет сохранять файлы, относящиеся к ней (рис.
4.2). Для продолжения диалога выбираем левой кнопкой мыши пункт “Далее>”.
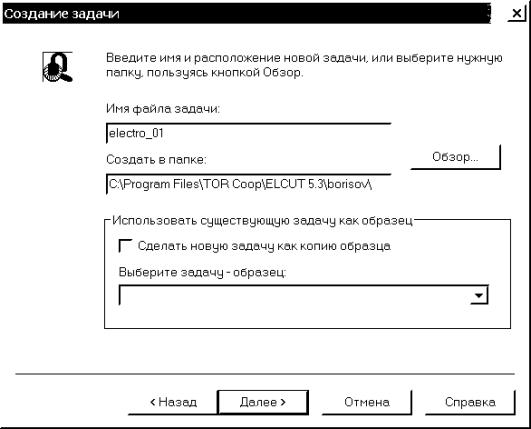
Рис. 4.2. Окно ввода имени и месторасположения задачи ELCUT
1.3. Появляется новое окно
“Ввод параметров новой задачи”. В графе тип задачи выбираем левой кнопкой мыши
- “Электростатическое поле”, класс модели - “Плоская”, расчет – “Обычный”.
Имеет смысл принять предложенные системой имена файлов модели и физических
свойств (рис. 4.3). Левой кнопкой мыши выбираем “Далее>”.
1.4. Появляется новое окно
“Выбор системы координат”. Выбираем левой кнопкой мыши “Единицы длины” –
сантиметры, “Система координат” – Декартовы координаты (рис. 4.4). Завершаем
диалог - “Готово”.
1.5. Появляется окно с
“деревом” (будем пользоваться в дальнейшем этой аббревиатурой) задачи
(располагается по умолчанию в левой части главного окна ELCUT) (рис. 4.5).
Рекомендуем сразу сохранить созданное описание новой задачи. Для чего нажимаем
одновременно комбинацию клавиш Ctrl+S или левой кнопкой мыши
вызываем меню Файл, из развернувшегося списка меню Файл выбираем команду
“Сохранить все файлы задачи”. Автоматически ELCUT запишет файл с расширением pbm в
выбранное согласно пункту 1.3 место на диске или другом носителе.
Рис. 4.3. Окно описания задачи ELCUT
Рис. 4.4. Окно выбора единиц измерения линейных размеров и системы координат задачи ELCUT
Рис. 4.5. Оконный интерфейс с “деревом” новой задачи ELCUT
2. Начало
работы с геометрической моделью
2.1. Двойной щелчок левой
кнопкой мыши на элементе “Геометрия: electro_01.mod” (см. рис. 4.5) “дерева”
задачи или одинарный на меню Правка, из развернувшегося списка выбираем левой
кнопкой мыши команду “Геометрическая модель”. Можно также выбрать команду
“Открыть” из контекстного меню, которое возникает при щелчке правой кнопкой
мыши на элементе “Геометрия: electro_01.mod ”.
2.2. Появляется диалоговое
окно ELCUT (рис. 4.6). Выбираем левой кнопкой мыши пункт “ОК”.
Рис. 4.6. Окно приглашения начать работу с геометрической моделью в ELCUT
2.3. Открывается окно
геометрической модели (рис. 4.7) и помимо общей панели инструментов появляется
дополнительная панель инструментов модели (ср. рис. 4.5 и рис. 4.7). При
дальнейшей работе следует помнить, что для работы в окне геометрической модели
или окне “дерева” задачи, нужно щелкнуть на соответствующем окне левой кнопкой
мыши (окно становится активным).
Рис. 4.7. Интерфейс новой задачи ELCUT с окном геометрической модели
3. Создание
геометрических элементов
3.1. При работе в окне
геометрической модели можно находиться в двух основных режимах: режиме выделения объектов (курсор мыши
в виде стрелочки), режиме вставки
вершин/ребер (курсор мыши в виде перекрестия при этом красной точкой выделяется
ближайший узел сетки привязки). В режиме вставки рисуются объекты
геометрической модели, при этом для выбора типа контура ребер следует
пользоваться соответствующей вкладкой на дополнительной панели инструментов модели
(см. рис. 3.7).
Наиболее удобно переходить
из одного режима в другой по клавише Insert или щелкнув левой кнопкой
мыши на соответствующей кнопке 
или 
дополнительной панели инструментов модели.
Можно также использовать команду “Режим вставки” из меню Правка.
3.2. Определимся с границами
расчетной области. Особых требований по условиям задачи нет, поэтому следует
исходить из физических особенностей задачи. Расчетная область может быть
представлена любой геометрической фигурой: квадратом, прямоугольником или
окружностью (в зависимости от геометрии задачи). Вполне достаточно, чтобы
границы расчётной области имели линейные размеры, превышающие размеры
исследуемого поля в 3-5 раз. Так как по условию задачи раздела 1.6 расстояние
между электродами составляет 0,8 м, расчетную область выбираем квадратом с
ребром 200 см и границами (-100 см £ х £ 100 см, 0 £ y £ 200 см). В дальнейшем все
координаты в сантиметрах.
3.3. На примере
рассматриваемой задачи покажем, как создавать расчетную область по вершинам в ELCUT. Чтобы
создать одиночную вершину вручную, следует в режиме вставки перевести курсор
мыши в узел сетки с требуемой координатой и сделать двойной щелчок левой
кнопкой мыши – в месте узла автоматически создастся вершина. Вводить вершины
можно вручную при создании ребер, при этом необходимо переводить курсор мыши в
нужные точки. В большинстве случаев для ввода вершин удобнее применять
соответствующее меню “Добавление вершин”.
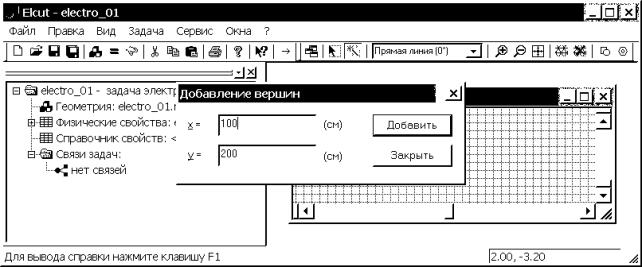
Введем четыре вершины
расчетной области и соединим их ребрами. Перейдем в режим вставки нажатием
клавиши Insert. Нажимаем правую кнопку мыши и в возникшем
контекстном меню (см. рис. 3.12) выбираем левой кнопкой мыши команду “Добавить
вершины” (рис. 4.8). Появляется окно “Добавление вершин” (см. рис. 3.11).
Рис. 4.8. Интерфейс новой задачи с контекстным меню режима вставки
Щелкнув левой кнопкой мыши в
соответствующих графах x и y, вводим с клавиатуры
координаты первой вершины (100, 0), затем “Добавить”. Вводим координаты других
вершин: (-100, 0), выбираем “Добавить”; (-100, 200), “Добавить”; (100, 200),
“Добавить” (рис. 4.9); далее “Закрыть”.
Рис. 4.9. Интерфейс новой задачи с окном создания вершин геометрической модели
Чтобы создать ребро, необходимо щелкнуть левой кнопкой мыши на вершине (если в данной точке вершины нет, она создастся вместе с ребром) и, удерживая левую кнопку, перевести курсор мыши ко второй вершине (при этом тип контура, соединяющий две вершины, задается во вкладке выбора типа контура ребра (см. рис. 3.7)). Ребро появится на экране сразу, как только будет отпущена левая кнопка мыши. Таким образом, поочередно соединяем четыре вершины и создаем границы расчетной области.
Безразлично, в каком
порядке создаются рёбра, также не имеет значения направление рёбер. Если точка,
которую необходимо выбрать, находится за пределами экрана, следует использовать
полосу прокрутки. Для удобства отображения вершин и ребер следует использовать
полосы прокрутки справа и внизу окна геометрической модели и кнопки 
. Нажав
кнопку 
“Показать все” на дополнительной панели
инструментов модели, получаем наиболее удобное отображение всей геометрии
модели (рис. 4.10).
Рис. 4.10. Картина, завершающая построение замкнутой
области моделирования задачи
Беспокоиться о возможных ошибках при построении не стоит, ненужные вершины и ребра можно удалить позже. Допустим, при создании ребра была совершена ошибка. Нажимаем клавишу Insert еще раз, чтобы завершить режим вставки и перейти в режим выделения объектов. Затем, удерживая клавишу Ctrl, выделяем левой кнопкой мыши все удаляемые объекты, они меняют свой синий цвет на красный. Отпускаем клавишу Ctrl. Нажимаем клавишу Delete или выбираем команду “Удалить выделенное” из меню Правка. Удаляемые объекты исчезают с экрана. Отметим, что отдельные вершины или ребра можно удалять и без использования клавиши Ctrl, удержание которой позволяет выделять более чем один объект.
В любом случае следует
помнить, чтобы выделить вершину, ребро или область необходимо щелкнуть
один раз левой кнопкой мыши по выделяемому объекту, чтобы снять выделение
следует щелкнуть вне этого объекта.
Замечание: при работе с геометрической моделью не забывайте перед тем, как
создавать новые объекты, сохранять уже созданную модель. Для этого можно
использовать комбинацию клавиш Ctrl+S или левой кнопкой мыши
вызываем меню Файл, из развернувшегося списка выбираем команду “Сохранить все
файлы задачи”. Можно также использовать команду “Сохранить как”. Автоматически ELCUT
сохраняет модели с расширением *.mod. Эта рекомендация касается
особенно низко-производительных персональных компьютеров, так как обработка
большого массива чисел ELCUT или некорректные действия
пользователя, могут приводить иногда к зависаниям пакета (стандартная ситуация
для любого приложения Windows).
3.4. В задачах по расчету
полей системы заряженных проводов в большинстве случаев можно пренебречь
геометрическими размерами электродов, так как сечения проводов много меньше,
чем расстояния между ними. Когда геометрические размеры электродов сопоставимы
с размерами всей модели, упростить задачу подобным образом нельзя. На примере рассматриваемой
задачи покажем, как создавать электроды с учетом формы их сечений в ELCUT.
Построим первый электрод как
окружность радиуса 1 см с центром в точке с координатами (0, 80). Для этого
создаем две вершины с координатами (-1, 80) и (+1, 80) или (0, 81) и (0, 79), что
не принципиально. Главное, чтобы эти две вершины отстояли от центра окружности
(0, 80) на 1 см. Затем во вкладке выбора типа контура ребра (см. рис. 3.7)
выбираем левой кнопкой мыши “Половина круга (180°)”. Используя кнопки
“Крупнее” и “Мельче” 
дополнительной панели инструментов модели,
выбираем наиболее удобное отображение созданных вершин. В режиме вставки соединяем
созданные вершины полуокружностями. Например, соединяем от вершины с
координатами (+1, 80) к (-1, 80), затем обратно от (-1, 80) к (+1, 80). Если совершена ошибка,
следуем приведенным ранее рекомендациям по устранению ошибок и пробуем снова.
Иногда в ELCUT после
ввода ребра с круглым контуром, пакет автоматически видоизменяет контур ребра
на многогранный (рис. 4.11). Это связано с тем, что автоматически заданный шаг
дискретизации в вершинах ребра слишком велик и его следует уменьшить. Для этого,
в приведенном примере, в режиме выделения объектов щелкнем левой кнопкой мыши
на одной вершине электрода, затем, удерживая клавишу Ctrl, на второй. Далее отпустив
клавишу Ctrl, нажмем комбинацию клавиш Alt+Enter. В появившемся окне
“Свойства выделенных объектов” изменим в графе “Шаг дискретизации” с
“Автоматический” на “Задан” и введем величину шага дискретизации 0.5 (см).
Нажимаем “OK”, чтобы завершить диалог.
При этом форма электрода видоизменяется на требуемую, а вокруг каждой из двух
вершины возникает дополнительная окружность (рис. 4.12), которая позволяет
приблизительно оценить шаг дискретизации. Чем больше шаг дискретизации, тем
больше радиус дополнительных окружностей и тем меньше расчетная точность
картины поля вблизи этих вершин.
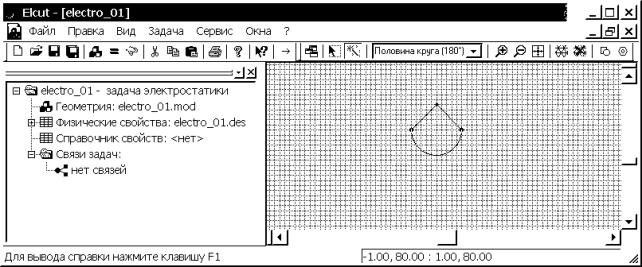
Рис. 4.11. Интерфейс
задачи и окно геометрической модели с примером предварительного
(грубого) изображения электрода
(окружности)
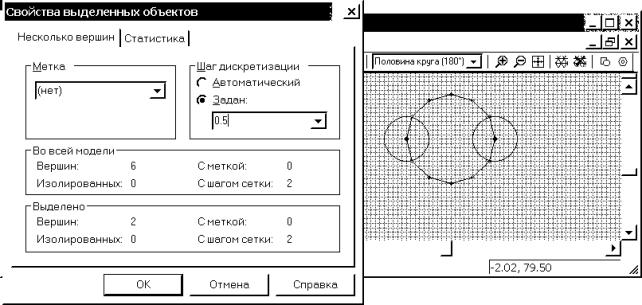
Рис. 4.12. Окна свойств и геометрической модели с примером уточненного (с заданным меньшим шагом дискретизации) изображения окружности электрода
Построим второй электрод как
окружность радиуса 1 см с центром в точке с координатами (0, 50). Нет
необходимости полностью создавать ее, нужно всего лишь сделать копию первой
окружности и перенести ее в точку с координатами центра второй окружности (0,
50). Для чего:
– Используя кнопки “Крупнее”
и “Мельче” дополнительной панели инструментов модели,
выбираем наиболее удобное отображение первой окружности;
– Перейдя в режим выделения,
перемещаем курсор мыши чуть выше и левее объекта, который хотим выделить (в
нашем случае это первая окружность). Щелкнем левой кнопкой мыши и, удерживая ее,
переводим курсор чуть ниже и правее объекта. При этом от места, с которого
начали, до места текущего положения курсора протянется черная рамка, которая
позволяет определить охватываемую область. Как только объект окажется в рамке,
отпускаем левую кнопку мыши и весь объект выделяется.
– Итак, объект полностью
выделен. Переводим курсор мыши на внутреннюю область объекта (первой
окружности) и нажимаем правую кнопку мыши. Появляется контекстное меню, из
которого левой кнопкой мыши выбираем команду “Дублировать выделенное”.
Возникает окно “Размножение объектов”. В разделе “Метод” оставляем тип действия
– “Перенос”, стоявший по умолчанию, в разделе “Вектор переноса”: графа ось х оставим 0, ось у вводим с клавиатуры –30, “Копий”: 1 (рис. 4.13). Выбираем левой
кнопкой мыши “ОК”, чтобы закрыть окно. Вторая окружность появится в заданном
месте с координатами центра (0, 50) на 30 см ниже по оси у, чем первая окружность с центром в точке (0, 80).
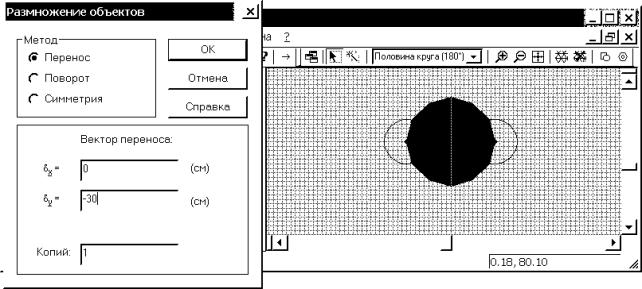
Рис. 4.13. Окно “размножения объектов” с выделенным в поле геометрической модели объектом размножения – окружности электрода
3.5. В рассматриваемой
задаче элементы двухпроводной линии в пространстве это стержни кругового
сечения, которые представляются в плоскости областями, ограниченными
окружностями с координатами вершин (0, 50), (0, 80) и радиусами 
= 1 cм.
Диаметры электродов более чем на порядок меньше характерных размеров модели, а
это позволяет считать реальные провода тонкими струнами и позволяет заменить
окружности на две точки в плоскости геометрической модели. Удаляем созданные
ранее окружности и создаем две вершины в плоскости модели с координатами (0,
50) и (0, 80) соответственно по аналогии с пунктом 3.3. Теперь структурно
геометрическая модель полностью завершена. Сохраняем ее нажатием комбинации
клавиш Ctrl+S. Автоматически ELCUT сохраняет геометрическую
модель с расширением *.mod.
В качестве приложения: В большинстве случаев
создание геометрии задачи упрощается, если воспользоваться возможностями
надстройки “Вставка фигуры”. Создадим расчетную область, используя эту надстройку.
Для ее вызова следует нажать комбинацию клавиш Ctrl+Alt+S, можно также
воспользоваться командой “Добавить Фигуру…” меню Правка или его контекстного
меню. Открывается соответствующее окно надстройки. Выбираем во вкладке “Фигура”
тип контура – прямоугольник (рис. 4.14). Щелкая левой кнопкой мыши в
соответствующих графах окна, вводим с клавиатуры: длина w=200, высота
h=200, центр в точке с координатами x=0, y=100, угол поворота вокруг
оси = 0, далее выбираем “Добавить” и затем “Закрыть”. Нажав кнопку “Показать все” на дополнительной панели
инструментов модели, получаем наиболее удобное отображение всей геометрии
модели (см. рис. 4.10).
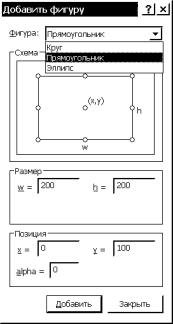
Рис. 4.14. Окно вставки фигуры заданной формы (здесь прямоугольника)
Для создания двух электродов
круглого сечения (т.е. при учете формы их сечений) также удобно воспользоваться
надстройкой “Вставка фигуры”. Для ее вызова
следует нажать комбинацию клавиш Ctrl+Alt+S, можно также
воспользоваться командой “Добавить Фигуру…” меню Правка или его контекстного
меню. Открывается соответствующее окно надстройки. Выбираем во вкладке “Фигура”
тип контура – круг (рис. 4.15). Щелкая левой кнопкой мыши в соответствующих
графах окна, вводим с клавиатуры: диаметр d=2, центр в точке с
координатами x=0, y=80, угол поворота вокруг
оси = 0, далее выбираем “Добавить”. Вводим данные для второго электрода: диаметр
d=2, центр в точке с координатами x=0, y=50, угол поворота вокруг
оси = 0, далее выбираем “Добавить” и затем “Закрыть”. Нажав кнопку “Показать все” на дополнительной панели инструментов
модели, получаем наиболее удобное отображение всей геометрии модели.
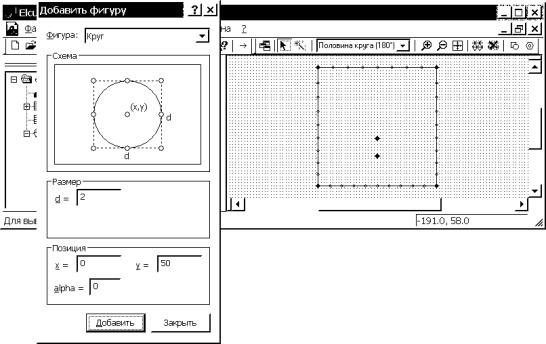
Рис. 4.15. Интерфейс задачи
с окном вставки фигуры заданной формы
(здесь круга)
В задачах с объектами
сложной формы возможностей надстройки “Вставка фигуры” бывает недостаточно, при
этом границы объектов приходится создавать по вершинам (как это описано в
пункте 3.3).
4. Задание
физических свойств
4.1. Первоначально задача
раздела 1.6 содержала две среды – воздух и землю и два электрода из однородного
материала. В такой постановке модель в ELCUT должна содержать три
замкнутых блока соответствующих среде (воздуху), первому и второму электродам.
Как среду землю в данном случае учитывать не приходится, следует определить
лишь граничное условие на ее поверхности, которое задается на соответствующем
нижнем ребре (см. далее). Упрощение посредством замены стержневых электродов
струнами привело к тому, что модель в ELCUT должна содержать только
один блок, соответствующий среде - воздуху.
4.2. Присвоим мнемоническое
имя “Воздух” для метки блока и зададим свойства среды, для чего дважды щелкнем
левой кнопкой мыши (в режиме выделения) на области, ограниченной ребрами,
созданными в пункте 3.3. Блок станет выделенным и появится диалоговое окно
“Свойства выделенных объектов”. Щелкнув левой кнопкой мыши в графе “Метка”,
вводим с клавиатуры имя метки – Воздух (рис. 4.16). В ELCUT возможно присвоение меткам
как англоязычных, так и русскоязычных названий. Шаг дискретизации оставляем
“Автоматический”. Выбираем “OK”, чтобы
завершить диалог. В окне “дерева” задачи, раздел “Физические свойства”,
подраздел “Метки блоков” появляется элемент “Воздух”.
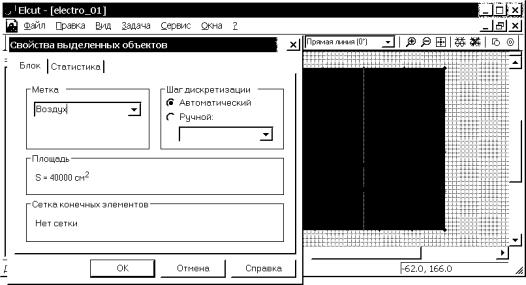
Рис. 4.16. Назначение имени (метки) выделенному блоку расчетной области
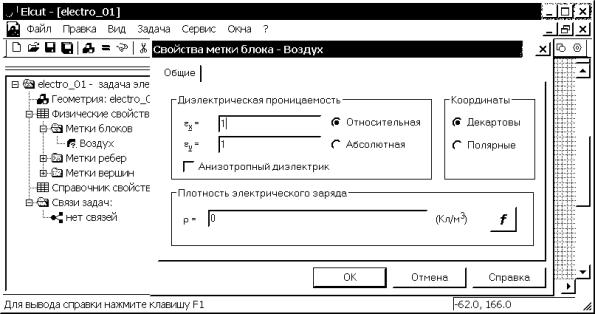
4.3. Дважды щелкнув левой
кнопки мыши на элементе “Воздух”, открываем окно “Свойства метки блока -
Воздух”. В разделе “Диэлектрическая проницаемость” выбираем графу 
и вводим с клавиатуры
– 1. Так как пункт “Анизотропный диэлектрик” не выбран, в графе 
автоматически
появляется 1. Оставляем выбранным пункты: “Относительная” раздела
“Диэлектрическая проницаемость” и “Декартовы” раздела “Координаты”. Плотность
электрического заряда r оставляем равной нулю (рис.
4.17).
Рис. 4.17. Назначение физических свойств блока с меткой Воздух
Выбираем “OK”, чтобы завершить диалог. Свойства среды в модели
теперь полностью определены.
5. Создание
меток ребер и вершин
5.1. Щелкнем левой кнопкой
мыши на окне геометрической модели, чтобы сделать его активным. Создадим метку
для верхнего ребра квадрата, ограничивающего расчетную область. В режиме
выделения, дважды щелкнем левой кнопкой мыши на верхнем ребре. Также можно
щелкнуть на ребре один раз, после чего нажать комбинацию клавиш Alt+Enter.
Появляется окно “Свойства выделенных объектов”. Щелкнув левой кнопкой мыши в
графе “Метка”, вводим с клавиатуры имя метки – Поле. Шаг дискретизации
оставляем “Автоматический”. Выбираем “OK”, чтобы завершить диалог (рис. 4.18). В окне “дерева” задачи,
раздел “Физические свойства”, подраздел “Метки ребер” появляется элемент
“Поле”.
Рис. 4.18. Назначение имени (метки) верхнего ребра – Поле. (Аналогично нижнего ребра - Земля)
Аналогично создаем метку
“Земля” для нижнего ребра квадрата, ограничивающего расчетную область.
5.2. Для присвоения метки
вершине соответствующей верхнему электроду, в режиме выделения дважды щелкнем
на ней левой кнопкой мыши. Появляется окно “Свойства выделенных объектов”.
Щелкнув левой кнопкой мыши в графе “Метка”, вводим с клавиатуры имя метки –
Потенциал 1. Шаг дискретизации оставляем “Автоматический”. Выбираем “OK”,
чтобы завершить диалог. В окне “дерева”
задачи, раздел “Физические свойства”, подраздел “Метки вершин” появляется
элемент “Потенциал 1”.
Аналогично создаем метку с
названием “Потенциал 2” для вершины соответствующей нижнему электроду (рис.
4.19). Знаки вопроса около меток ребер и вершин в окне “дерева” задачи
указывают на то, что граничные условия на соответствующих элементах еще не
определены.
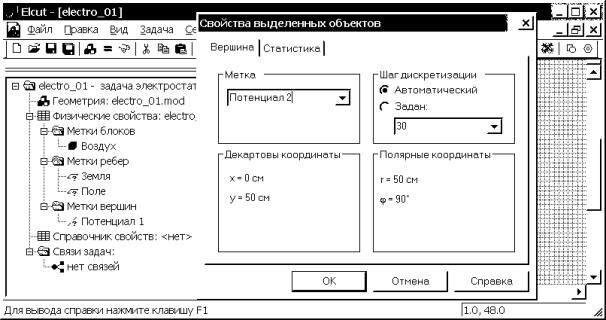
Рис. 4.19. Задание имен (меток) вершин электрических осей электродов: верхнего - Потенциал 1, нижнего - Потенциал 2
Создание меток ребер и
вершин закончено, теперь можно задавать граничные условия.
6. Задание
граничных условий
6.1. Метки рёбер и вершин
используются для задания граничных условий на внешних границах объектов и
внутренних границах области. В рассматриваемом случае нужно задать граничные
условия на ребрах с метками “Земля”, “Поле” и в вершинах с метками “Потенциал
1”, “Потенциал 2”.
6.2. Поверхность земли, как
любого однородного проводника, представляет собой эквипотенциальную
поверхность. Дважды щелкнув левой кнопкой мыши на элементе “Земля” “дерева”
задачи, открываем окно “Свойства метки ребра - Земля”. Потенциал ребра с меткой
“Земля” известен заранее и равен нулю, что описывается граничным условием
Дирихле. В квадратике напротив “Потенциал” ставим левой кнопкой мыши галочку. В
графе оставляем нуль. Нажимаем “OK”, чтобы
завершить диалог.
6.3. Определим поле,
создаваемое по условию задачи грозовой тучей. Для этого на ребре с меткой
“Поле” задается граничное условие Неймана. Определим 
- плотность зарядов
на поверхности тучи по формуле:
(
).
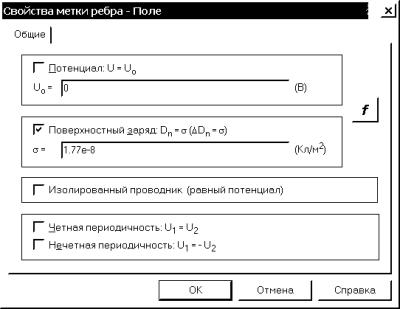
Дважды щелкнув левой кнопкой мыши на соответствующем элементе “дерева” задачи, открываем окно “Свойства метки ребра - Поле”. В квадратике напротив “Поверхностный заряд” ставим левой кнопкой мыши галочку. Щелкнув левой кнопкой мыши в графу, вводим с клавиатуры соответствующее число (рис. 4.20). При вводе необходимо использовать англоязычную раскладку клавиатуры и вводить числа через точку, иначе система выдаст сообщение об ошибке. Нажимаем “OK”, чтобы завершить диалог.
Рис. 4.20. Окно задания граничного условия Неймана для ребра с меткой Поле
6.4. Для вершин с метками
“Потенциал 1” и “Потенциал 2” задаются условия Дирихле в соответствии с данными
задачи.
Дважды щелкнув левой кнопкой
мыши на элементе “дерева” задачи “Потенциал 1”, открываем окно “Свойства метки
вершины - Потенциал 1”. В квадратике напротив графы “Потенциал” ставим левой
кнопкой мыши галочку. Щелкнув левой кнопкой мыши в графу, оставляем в ней число
0. Нажимаем “OK”, чтобы завершить
диалог.
Дважды щелкнув левой кнопкой
мыши на элементе “дерева” задачи “Потенциал 2”, открываем окно “Свойства метки
вершины - Потенциал 2”. В квадратике напротив графы “Потенциал” ставим левой
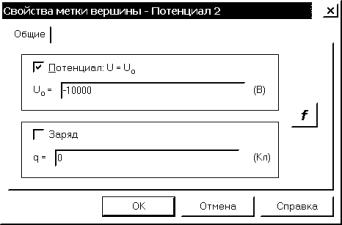
кнопкой мыши галочку. Щелкнув левой кнопкой мыши в графу, вводим с клавиатуры
число –10000 (рис. 4.21). Нажимаем “OK”, чтобы
завершить диалог.
Рис. 4.21. Окно задания граничного условия Дирихле для оси с меткой Потенциал 2
На боковых рёбрах выделенной
области (слева и справа) автоматически устанавливаются однородные граничные условия – (
= 0), так как им не присвоены метки с именами. Это на самом
деле имеет место в данной задаче, так как силовые линии поля в области,
удалённой от двухпроводной линии, определяются только вертикальной составляющей
поля тучи (тангенциальной к ребрам).
Теперь файл описания
физических свойств полностью готов и его следует сохранить (Ctrl+S). ELCUT
сохраняет файл описания физических свойств (для электростатики) с расширением
*.des.
7. Построение
расчетной сетки
7.1. Для построения
расчетной сетки активизируем окно геометрической модели, щелкнув на ней левой
кнопкой мыши. Нажимаем кнопку 
“Построение сетки” на дополнительной панели
инструментов модели или можно воспользоваться командой “Построить сетку” из
списка меню Правка. В модели автоматически создается расчетная сетка (рис. 4.22).
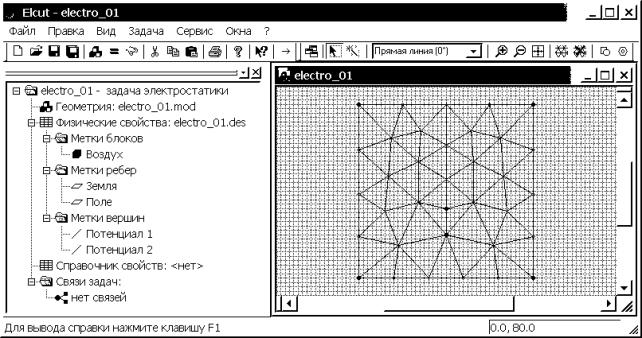
Рис. 4.22. Пример первичного автоматического построения расчетной сетки
В студенческой версии ELCUT 5.3
налагается ограничение на число узлов расчетной сетки – 255 узлов (в
профессиональной версии таких ограничений нет). Можно проверить насколько
оптимально используется ресурс 255 узлов, для чего следует нажать комбинацию
клавиш Alt+Enter при активном окне геометрической модели. В
появившемся окне “Свойства выделенных объектов”, присутствует единственный
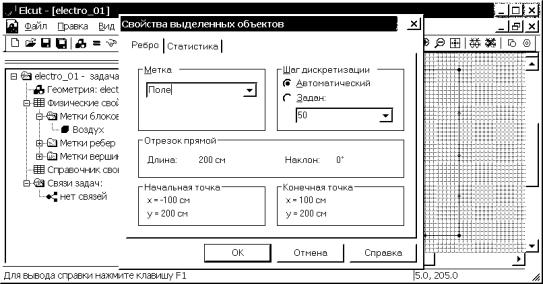
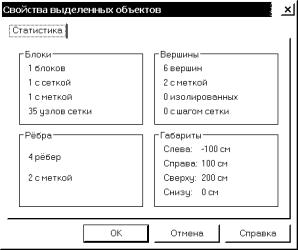
раздел “Статистика”. В графе “Блоки” смотрим количество узлов сетки (рис.
4.23). Из 255 узлов используется только 35, таким образом, ресурс использован
не оптимально. Закроем окно “Свойства выделенных объектов”.
Рис. 4.23. Информационное окно о геометрии выделенных объектов и числе узлов расчетной сетки
7.2. Для повышения точности
расчета количество используемых узлов нужно увеличить, для чего следует
задавать шаг дискретизации вручную. В рассматриваемой задаче можно предположить
существенную неоднородность поля вблизи элементов двухпроводной линии, так что
густота сетки в этих местах должна быть максимальной. Щелкнем левой кнопкой
мыши на одной вершине, затем, удерживая клавишу Ctrl, на второй. Далее отпустив
клавишу Ctrl, нажмем комбинацию клавиш Alt+Enter. В появившемся окне
“Свойства выделенных объектов” изменим в графе “Шаг дискретизации” с
“Автоматический” на “Задан” и введем величину шага дискретизации 4 (см).
Нажимаем “OK”, чтобы завершить диалог.
Расчетная сетка исчезает, а
вокруг каждой из двух вершин возникает дополнительная окружность, которая
позволяет приблизительно оценить шаг дискретизации. Чем больше шаг
дискретизации, тем больше радиус дополнительных окружностей и тем меньше
точность картины поля вблизи этих вершин.
7.3.
Выделим четыре вершины в углах расчетной области и зададим шаг дискретизации
равным 20 (см). Нажимаем кнопку “Построение сетки” на дополнительной панели
инструментов модели. В студенческой версии ELCUT 5.3 появится информационное
окно “Превышено ограничение на число узлов (255)”. Для того чтобы продолжить
работу, нажимаем “OK” (рис. 4.24).
Изменять значение шага дискретизации следует
на границах расчетной области, где картина поля почти однородна. Снова выделяем
четыре вершины в углах расчетной области и задаем шаг дискретизации равным 23
(см). Нажимаем кнопку “Построение сетки” на дополнительной панели
инструментов модели. Расчетная сетка создана. Нажав комбинацию клавиш Alt+Enter,
проверяем число используемых узлов сетки, их 236 (рис. 4.25). Такое количество
узлов вполне приемлемо, теперь возможно решить задачу и посмотреть результаты
решения. Работа с моделью закончена, и её следует сохранить.
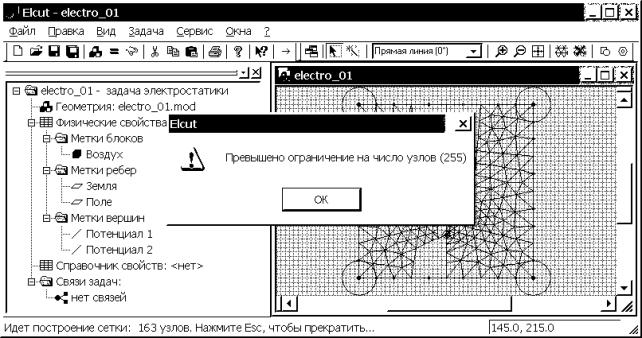
Рис. 4.24. Интерфейс задачи с информационным окном о превышении возможного числа узлов расчетной сетки
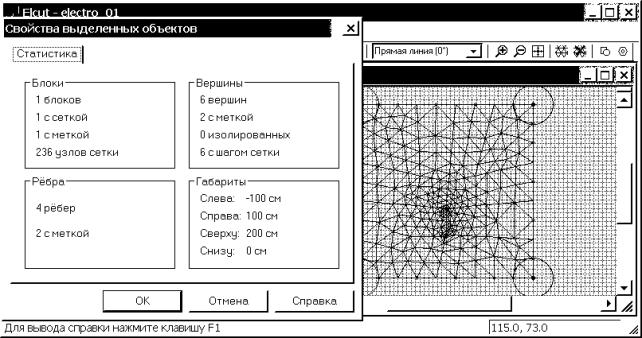
Рис. 4.25. Окончательный вариант расчетной сетки конечных элементов с окном статистики объектов
8. Визуализация
результатов решения
8.1. Для решения задачи щелкаем
левой кнопкой мыши на кнопке “Решить” 
общей панели инструментов, можно также
воспользоваться командами
“Решить: …” или “Анализ результатов” меню Задача (в последнем случае система
предложит сначала решить задачу, поскольку решение пока отсутствует). Если
после сохранения задачи в ней были произведены какие-либо изменения, ELCUT
предложит сохранить изменения, выбираем “Да”. После утвердительных ответов на
все информационные сообщения системы, когда решение закончится, автоматически
откроется окно результатов решения, в котором будет отражена картина поля (рис.
4.26).
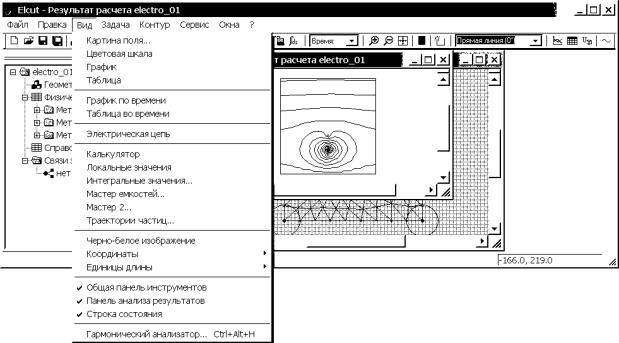
Рис. 4.26. Решение задачи с окном результатов расчета и открытым меню Вид
При активном окне “Результат
расчета” появятся дополнительное меню Контур, панель анализа результатов, изменятся
команды меню Вид. Пакет ELCUT предоставляет множество
способов изображения и анализа картины поля, укажем основные из них.
8.2. Щелкнем левой кнопкой
мыши на меню Вид, далее выбираем “Картина поля…”, после чего появляется
соответствующее окно “Картина поля” (рис. 4.27). В окне выбираются параметры
поля, которые необходимо отобразить. Если среди остальных режимов выбран
“Цветная карта”, то автоматически активируется кнопка 
“Цветовая шкала” на панели анализа
результатов, щелчок по которой левой кнопкой мыши вызывает соответствующую
шкалу или можно воспользоваться меню Вид, далее “Цветовая шкала”.
8.3. Активация кнопки 
“Добавить к контуру” на панели анализа
результатов (можно также использовать команду “Добавить” меню Контур) позволяет
в ручном режиме вводить линии (для отображения графика изменения каких-либо
параметров поля вдоль них или создания таблицы данных) или выделять контуры (по
которым вычисляются интегральные характеристики). При ручном вводе следует
щелкнуть левой кнопкой мыши на начальной точке линии в окне результатов
расчета, затем, удерживая левую кнопку мыши, перевести курсор до конечной точки
и отпустить кнопку мыши.
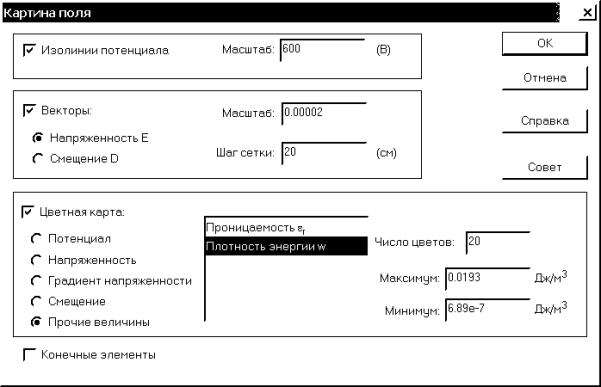
Рис. 4.27. Окно выбора отображаемых параметров поля
Для ввода контура строят
первую линию и от ее конца ведут следующую и т.д. пока контур не замкнется.
Иногда удобно использовать команду “Замкнуть” меню Контур или команду “Замкнуть
контур” из списка команд контекстного меню. Любой контур имеет направление
обхода, которое отражается стрелкой при каждой линии, ограничивающей его.
При создании линий можно
задавать тип их контура: прямая линия, четверть круга, половина круга, три
четверти круга, в соответствующей вкладке “Раствор дуги” на панели анализа
результатов.
Для редактирования созданных
линий и контуров, их удаления или смены направления обхода пользуются командами
меню Контур или вызывают правой кнопкой мыши контекстное меню и выбирают
соответствующую команду (рис. 4.28).
Для точного ввода начальных
и конечных координат линий или контуров следует вызвать окно “Добавление линий”
через меню Контур, где выбираем “Ввод линий…” или через контекстное меню,
выбрать команду “Ввод линий контура…”.
8.4. В качестве примера
построим график изменения потенциала при х
= 0 вдоль оси у. Для точного задания
начала и конца линии, щелкнув правой кнопкой мыши в окне результатов расчета,
из контекстного меню выбираем команду “Ввод линий контура…”. Первая точка имеет
координаты (0, 0), нажимаем левой кнопкой мыши на пункт “Начальная точка”.
Пункт “Начальная точка” сменяется пунктом “Добавить линию”. Вводим с клавиатуры
координаты второй точки (0, 200) и нажимаем левой кнопкой мыши на пункт
“Добавить линию” (рис. 4.29). Выбираем “Закрыть”, чтобы завершить диалог.
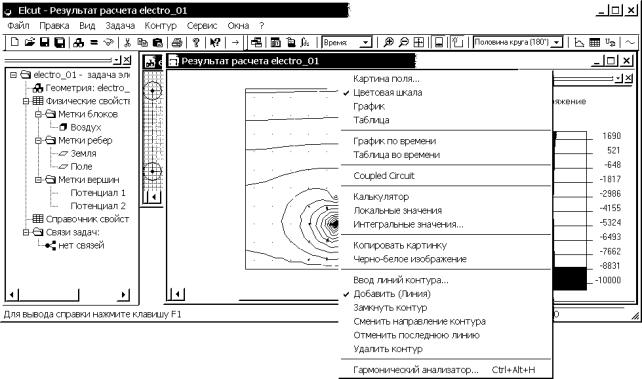
Рис. 4.28. Интерфейс задачи с контекстным меню окна результатов расчета
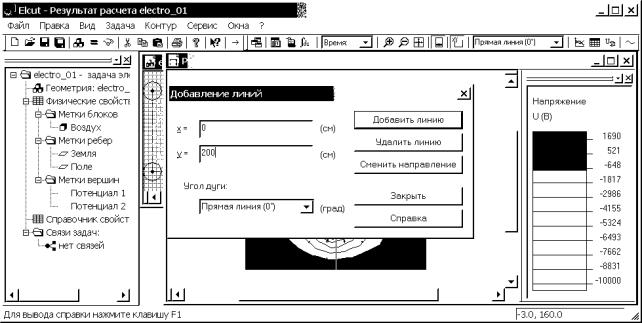
Рис. 4.29. Пример назначения линии исследования характеристик поля
При создании линии или
контура автоматически активизируются кнопки “График” и “Таблица” панели анализа
результатов 
. Нажатие
левой кнопкой мыши любой из них вызывает соответствующее окно. График изменения
потенциала при х = 0 вдоль оси у представлен на рис. 4.30.
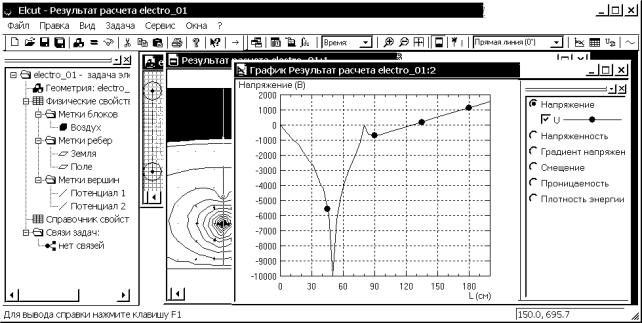
Рис. 4.30. Пример вывода в ELCUT графика потенциальной функции
вдоль оси у при х = 0
Помимо потенциальной функции
можно вывести графики изменения других параметров поля вдоль выбранной линии.
График картины поля и таблица результатов расчета выводятся в отдельных окнах.
Для возвращения к окну результатов расчета или к окну геометрии модели используется
комбинация клавиш Ctrl+Tab (см. раздел 3.3 – Меню Окна).
Сравнивая рисунки 4.30 и
1.12, можно судить о хорошем совпадении результатов. Отметим, что относительная
погрешность расчета в ELCUT определяется числом узлов
расчетной сетки и возрастает в областях с малым числом узлов (в рассматриваемом
случае на границах расчетной области).
8.5. Используя кнопку
“Локальные значения” панели анализа результатов 
, можно
определить величины параметров поля для любой указанной точки. Щелчок левой
кнопкой мыши на кнопке 
вызывает окно Калькулятора, при этом под разделом “Локальные значения” появится
строка с сообщением “Укажите точку…”. Следует перевести курсор мыши на желаемую
точку в окне результатов расчета, при этом курсор мыши со стрелки изменит форму
на 
, и
щелкнуть левой кнопкой мыши. Автоматически ELCUT выдаст всю информацию о точке.
Координаты точки можно задать точно, выбрав соответствующую команду из
контекстного меню (рис. 4.31) или щелкнув левой кнопкой мыши на надпись “x = …” или
“у = …” и нажав Enter. Далее вводятся обе координаты через запятую или
двоеточие.
Для возвращения к режиму
ввода и редактирования контуров следует щелкнуть левой кнопкой мыши на кнопке .
8.6. Используя кнопку 
“Интегральный калькулятор” на панели анализа
результатов, можно определить интегральные величины для любого замкнутого
контура.
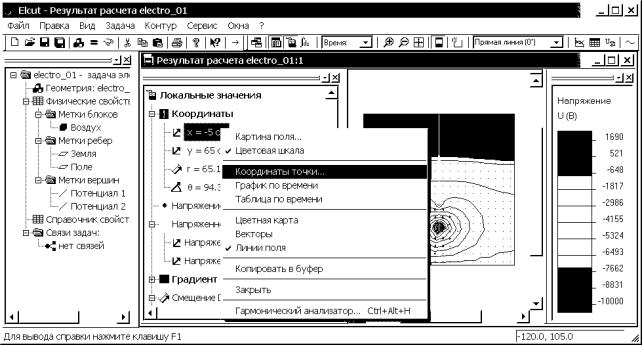
Рис. 4.31. Пример вывода информации о физических параметрах поля в заданной точке исследуемой области
Допустим, какой-либо контур
или линия уже созданы – удалим их, затем построим новый замкнутый контур. Щелкнем
левой кнопкой мыши на окне результатов расчета, затем нажмем правую кнопку
мыши. Из появившегося списка команд контекстного меню выбираем “Удалить контур”
и линия или контур удаляется.
Создадим замкнутый контур с
типом линий, например, полуокружность вокруг верхнего электрода. Для точного
задания начала и конца контура, щелкнув правой кнопкой мыши в окне результатов
расчета, из контекстного меню выбираем команду “Ввод линий контура…”. Выбираем
соответствующий тип контура линий в графе “Угол дуги” – Половина круга (180°).
Вводим с клавиатуры координаты точки (0, 48), нажимаем пункт “Начальная точка”,
затем вводим координаты (0, 52), нажимаем пункт “Добавить линию”, вводим
координаты (0, 48), нажимаем пункт “Добавить линию”. Выбираем “Закрыть”,
чтобы завершить диалог. Создался
замкнутый контур. Кнопки “Крупнее” и “Мельче” дополнительной панели инструментов модели
позволяют наиболее удобным образом отобразить контур. Щелкнув левой кнопкой
мыши на кнопке , получаем
информацию об интегральных характеристиках (рис. 4.32).
8.7. Покажем последовательность шагов, необходимых для
определения емкости системы проводников в ELCUT. Щелкнув левой кнопкой мыши на меню Вид, выбираем
“Мастер емкостей”, и он стартует. Внимательно знакомимся с информацией на
первой странице (рис. 4.33). Выбрав “Далее”, переходим на следующую страницу.
Выбираем левой кнопкой мыши из списка проводников, расположенного в правой
части окна, проводник с меткой “Потенциал 2”. Выбираем “Далее”, чтобы
продолжить диалог (рис. 4.34). В открывшемся окне левой кнопкой мыши выбираем
созданный в предыдущем параграфе замкнутый контур (рис. 4.35). Чтобы
воспользоваться альтернативным способом вычисления емкости, следует нажать
кнопку “Вычислить энергию”. Выбираем “Далее”, чтобы продолжить диалог. На
завершающей странице приводятся результаты расчета (рис. 4.36).
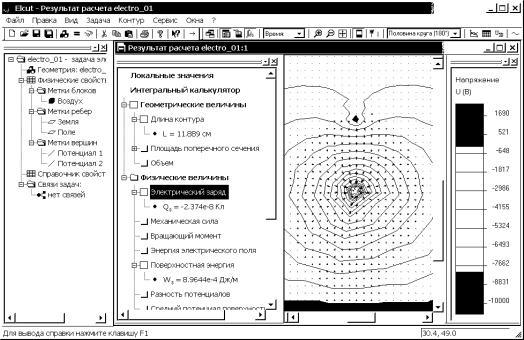
Рис. 4.32. Пример вывода интегральных характеристик поля
Рис. 4.33. Информационное окно вычисления емкостей системы электродов
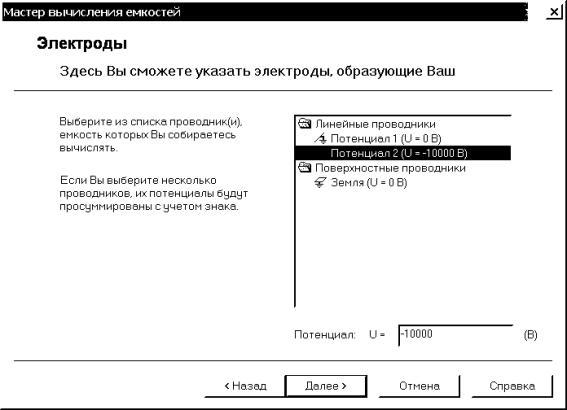
Рис. 4.34. Окно выбора системы проводников с известным потенциалом
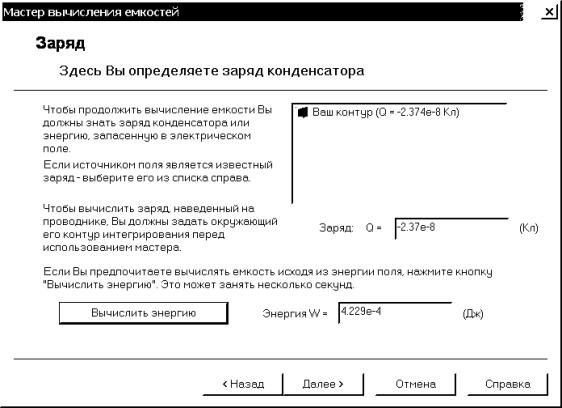
Рис. 4.35. Окно выбора расчетного контура
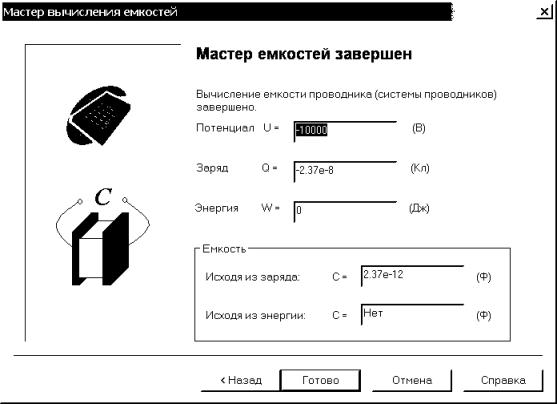
Рис. 4.36. Окно результатов расчета мастера емкостей
После завершения работы мастера вычисления емкостей его можно запустить повторно, дважды щелкнув левой кнопкой мыши на соответствующем разделе в окне результатов. Отметим, что в плоскопараллельной задаче все источники поля задаются через удельные значения на один метр (например, заряд проводника). Поэтому, результирующая емкость тоже исчисляется как погонная, т.е. на 1 метр, и измеряется в Ф/м.
Используем также возможности надстройки, позволяющей вычислять собственные
и взаимные частичные емкости в задачах электростатики. Если эта надстройка не
включена в список меню Сервис, то ее необходимо подключить вручную (см. раздел
3.3 – Меню Сервис). Вызываем
надстройку соответствующей командой из меню Сервис (рис. 4.37). Если в ELCUT открыто две или более задачи электростатики, то в
левом списке окна “Матрица емкостей” следует выбрать интересующую задачу. При
этом в списке проводников (справа) появится перечень всех меток ребер и вершин
задачи.
Щелчком левой кнопки мыши в колонке “Сведения” можно установить или снять
заземление любого из проводников. Заземление означает, что потенциал
соответствующего проводника равен нулю и для него не вычисляются частичные
емкости.
Убрав флажок слева от имени метки, можно исключить её
из расчета. Исключение означает, что метка не будет участвовать в вычислении
матрицы емкостей, но, в отличие от заземления, ей не будет приписан нулевой
потенциал.
Сформировав список проводников, участвующих в расчете,
нажимаем кнопку “Вычислить”. Система
автоматически производит решение и выдает его результат (см. рис. 4.37). В
результатах расчета под заголовком “Список
проводников” перечислены проводники с присвоенными им порядковыми
номерами. Далее идут результаты вычисления энергии в частных задачах, затем приводится
матрица коэффициентов электростатической индукции, и ниже, под заголовком “Собственные и взаимные частичные емкости”,
- матрица собственных и частичных емкостей. Чтобы найти соответствие между
номером проводника и его меткой, следует пользоваться списком проводников.
Рис. 4.37. Окно надстройки для вычисления собственных и взаимных частичных емкостей в задачах электростатики
Задача решена. Для
завершения сеанса следует закрыть все окна. Если после предыдущего сохранения
задачи в ней были произведены какие-либо изменения, то ELCUT предложит сохранить
изменения. Для их сохранения следует выбрать “Да”. Выход из пакета осуществляется через меню Файл команда “Выход”.
При новом запуске пакета все созданные ранее задачи могут быть вызваны через
команду “Открыть” меню Файл.